[알고리즘 ] 동적 계획 법 (Dynamic Programming/DP)
동적 계획법이란?
- 큰 의미에서 분할 정복과 같은 접근 방식을 의미.
- 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한 답을 계산해 내기 때문.
- 두번 이상 반복 계산되는 부분 문제들의 답을 미리 저장함으로써 속도의 향상을 꾀하는 알고리즘 설계기법을 동적 계획법이라고 한다.
하지만! 모든 문제를 이렇게 풀 수 없고 특별한 속성이 필요하다.
사용방법 :
1. 문제를 부분 문제로 나눈다.
2. 가장 작은 부분 문제부터 해를 구한 뒤 테이블에 저장.
3. 테이블에 저장되어 있는 부분 문제의 해를 이용하여, 점차적으로 상위 부분 문제의 최적해를 구한다.
사용 조건 :
1, 최적 부분 구조 : 큰 문제를 작은 문제로 나눌 수 있습접니다.
2. 중복되는 부분 문제 : 동일한 작은 문제를 반복적으로 해결 합니다.
접근 방법:
- 주어진 문제가 동적 계획법 유형임을 파악 하는 것이 중요.
- 가장 먼저 그리디, 구현, 완전 탐색등의 아이디어로 문제를 해결 할 수 있는 지 고려.
- 우선 비효율적인 완전탐색 알고리즘을 이용해서 프로그램을 작성 한뒤, 작은 문제에서 구한 답이 큰 문제에서도 사용 할 수 있으면, 코드를 개선 하는 방향으로 적용
* 한번 계산한 값을 저장해 뒀다가 재활용 하는 최적화 기법을 메모이제이션이라고 한다.
수학의 함수에서는 입력이 정해져 있으면 출력도 정해져 있다. 하지만 프로그래밍에서의 함수는 이러한 속성이 적용되지 않는다. 함수의 입력 외에도 전역 변수, 입력 파일, 클래스의 멤버변수 등 수 많은 입력이 존재한다.
함수의 반환 값이 그 입력 값만으로 결정되는지의 여부를 유식하게 참조적 투명성(referential transparency)라고 한다. 그리고 메모이제이션은 참조적 투명 함수의 경우에만 적용 할 수 있다.
동적계획법을 입문하는데 있어서 쉬운예는 피보나치 수열이다. 재귀함수를 구현하는 예제로도 좋은 예이다.
사용 예시
1.적용 전
피보나치 수열를 예로 확인해보자.
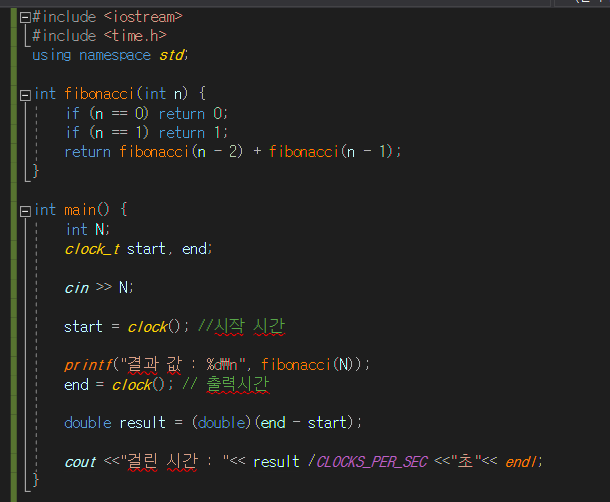
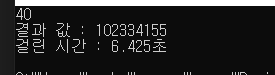
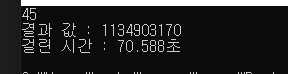
입력 값이 30이하라면 시간이 상관 없지만 그 이상이 된다면 시간이 점차 증가 된다.
이제 이렇게 오래 걸리는 이유를 한번 보면,
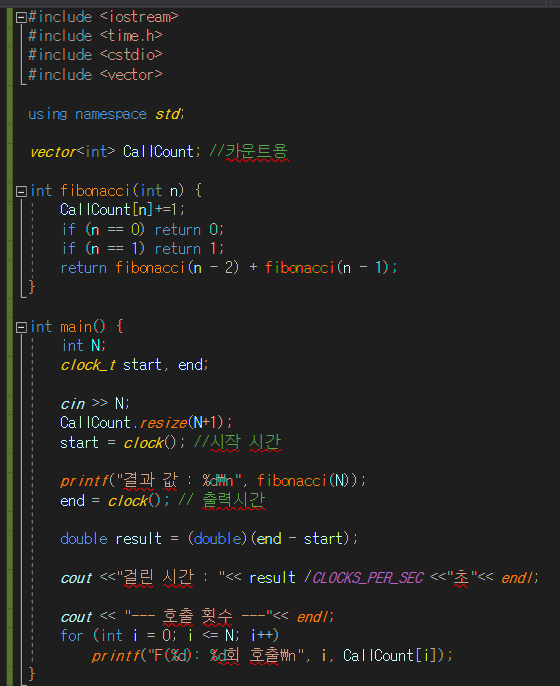
각 수가 몇번씩 실행되는지 확인하기 위한 CallCount 벡터를 추가해보았다.
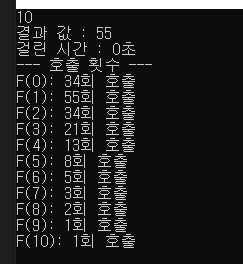
10을 넣어서 보면 F(0)이 34번이나 실행되고 F(1)이 55번이나 호출 되는것을 확인 해 볼수 있다.
큰 수 30을 확인해보면 호출 횟수가 어마어마하게 커진다.
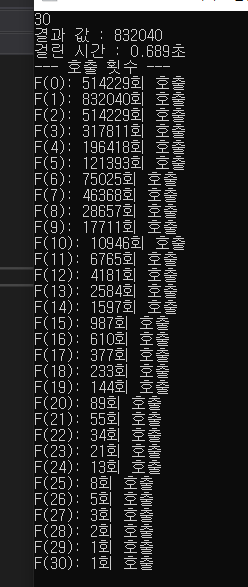
즉, 쓸데 없이 중복 계단을 반복하게 된다.
2. 하향식 동적 프로그래밍(top-down) 사용
이러한 불필요하게 재호출되는 문제 때문에 생기는 것을 막기 위해 메모이제이션(memoization)기법(하향식 동적 프로그래밍)을 사용한다.
https://ko.wikipedia.org/wiki/%EB%A9%94%EB%AA%A8%EC%9D%B4%EC%A0%9C%EC%9D%B4%EC%85%98
메모이제이션 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 메모이제이션(memoization)은 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여
ko.wikipedia.org
메모이제이션은 쉽게 말해, 계산결과를 캐시에 저장해두고, 나중에 재사용하는 기법으로 최적화, 캐싱 기법중 하나이다.
위에 피보나치수열 예에 dp라는 vector를 추가 해주어 캐싱해보자.
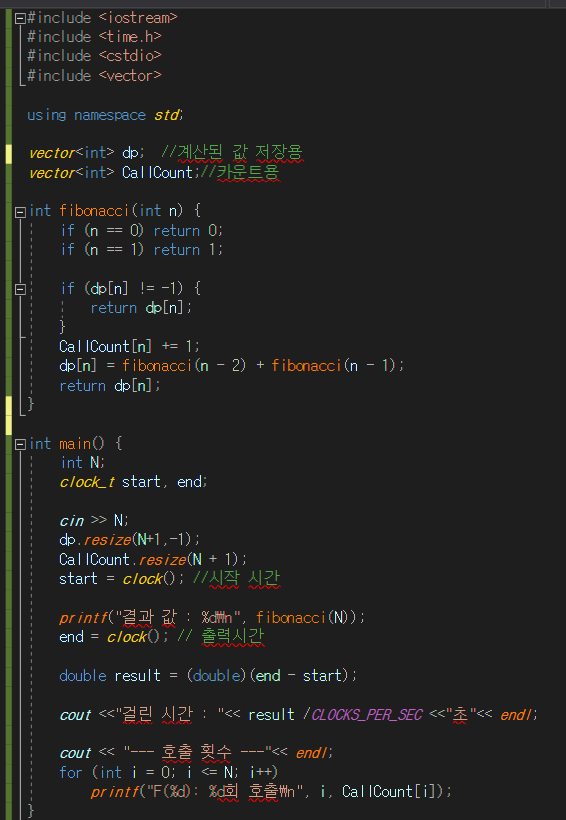
피보나치계산한 값으로 dp에 대입하고, 재귀 함수 진행 시 -1 이 아닌 수(이전에 캐싱된 값이 있다면)는 계산하지 않고 즉시 리턴해주게 된다. 이미 호출 된 값들을 저장하게 되면 아까와 같은 30을 호출하더라도
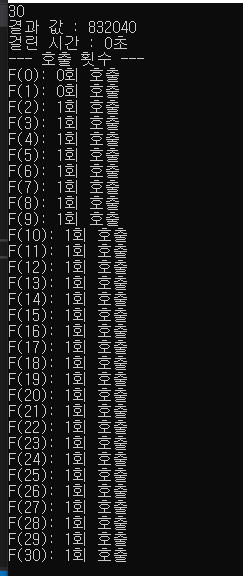
단 한번씩 호출(0, 1은 제외)되며 시간은 0초가 걸린다.
아까 위에서 메모이제이션 사용하기전 일반 재귀함수 호출에서는 70.588초가 걸렸던 시간이.

메모이제이션 사용 후에는 0초가 되었다.

본래 메모이제이션을 사용전에는 지수 시간복잡도로 발생되며 메모이제이션을 적용하게 난 뒤로는 O(n)시간 복잡도를 가진다.
하지만 단점으로 재귀호출이 한번 일어날때마다 스택에 새로운 층이 생기면서 공간 복잡도가 늘어나게 되는 단점이 있다. 원래는 별도의 메모리가 필요 없었지만, 이제는 각 항의 값을 기억하고 있어야 하므로 O(n)의 메모리가 필요하게 된다. 그래서 재귀적 알고리즘(recursive)말고 순환적(iterative) 알고리즘으로 구현하는 것이 더 낫다.
모든 재귀적 알고리즘은 순환적으로 구현될 수 있지만, 순환적으로 구현된 코드는 때로 훨씬 더 복잡하기도 하다.
3. 상향식 동적 프로그래밍 사용
상향식 동적프로그래밍으로 풀어보자면
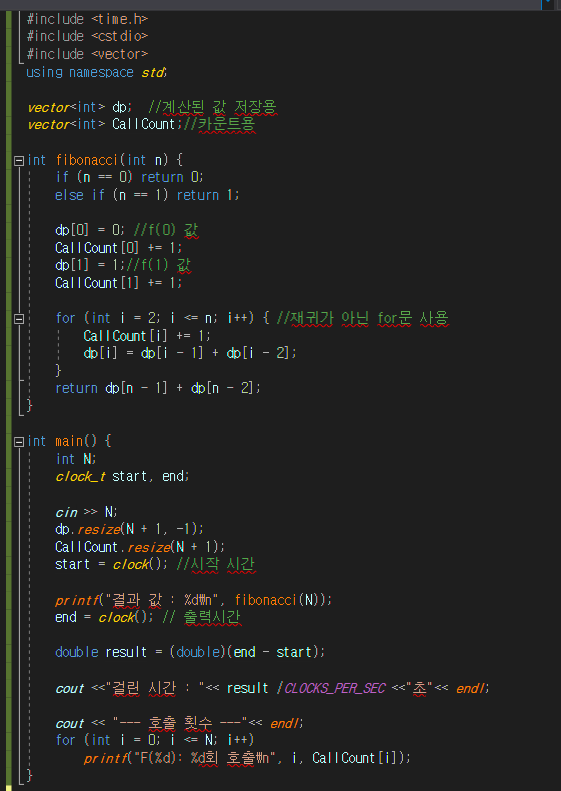
재귀함수를 사용하지 않고 finonacci 함수내에서 for문으로 확인한다.
결과는

그외 동적 계획법으로 풀 수 있는 문제들
- 최단 경로 찾기(다익스트라 알고리즘)
- 부분집합 합
- 연속 행렬 곰셉..등등..