[알고리즘] 플로이드 와샬(Floyd Warshall) 알고리즘이란? / C++
[알고리즘] 최단 경로찾기 ? 다익스트라 알고리즘 (Dijkstra Algorithm)
다익스트라 알고리즘은 프림 알고리즘 과 동작방식이 비슷하다. 다만 프림알고리즘은 단순히 간선의 길이를 이용해 어떤 간선을 먼저 연결할지 결정하는데 반해, 다익스트라 알고리즘은 '경로
hyo-ue4study.tistory.com
다익스트라 알고리즘과 비교
다익스트라 알고리즘은 하나의 정점에서 출발해서, 출발한 정점을 제외한 다른 모든 정점으로 가는 최단 경로를 구하는 알고리즘이다.
하지만, 모든 정점에서 다른 모든 정점으로 가는 최단 경로를 구하는 플로이드 와샬 알고리즘이 있다.
다익스트라 알고리즘은 가장 적은 비용을 하나씩 선택해야 했다면,
플로이드 와샬 알고리즘은 기본적으로 '거쳐가는 정점' 기준으로로 알고리즘을 수행한다는 점이 특징이다.
플로이드 와샬 알고리즘은 다이나믹 프로그래밍(DP) 기법에 의거한다.
아래와 같은 그래프 노드 와 가중치 간선이 있다고 하자,

노란색 글자 번호 노드에서 빨간색 번호 노드로 가는 비용을 나타내는 테이블도 있다.
자기 자신은 0이고 갈수 없다면 무한으로 적은 테이블은 '현재까지 계산된 최소비용'을 나타낸다.
우선 노드 1을 거쳐가는 경우부터 확인해보자
그럼 이제 초록색 표시 된 부분들을 아래와 같은 식으로 계산 해보아야 한다.

A에서 B로 가는 최소 비용 vs (A에서 노드 1로 가는 비용 + 노드 1에서 노드 B로 가는 비용)
2에서 3 가는 비용 확인
원래비용은 12 이다. 1을 거쳐 가려고 했을 때, 2에서 1까지는 4이고, 1에서 3까지는 7이다. 4+7=11이고,
원래비용 12 vs 1노드 경유 11이다. 1노드 경유 값이 더 작으므로 11로 갱신된다.
2에서 4로 가는 비용 확인
원래 비용은 13이고, 1을 경유하면, 2에서 1은 4이고, 1에서 4로 가는 비용은 무한이다.
원래 비용 13 vs 1노드 경유 4+무한이다. 더 적은 13을 그대로 둔다.
3에서 2로 가는 비용 확인
원래 무한의 비용이고, 1을 경유한다면, 6과 5가 든다. 총 11이고 무한과 11이므로 더 적은 11로 갱신된다.
3에서 4로 가는 비용 확인
원래 20이고, 1을 거쳐간다면 6+무한이다. 20vs무한+6 이므로 20을 그대로 둔다.
4에서 2로 가는 비용 확인
4에서 3로 가는 비용 확인
위 2가지 경우는 4에서 1로 가는 경우가 무한이므로 원래의 값이 낮거나 똑같이 무한이므로 그대로 두어준다.
이렇게 노드 1를 거치는 비용을 계산해보고 테이블을 갱신해준다.


2. 노드 2를 거쳐갈때

위의 초록색 부분이 갱신되어야 한다.
A에서 B로 가는 최소 비용 vs (A에서 노드 2로 가는 비용 + 노드 2에서 노드 B로 가는 비용)
이전과 같이 갱신해주면,

노란색 부분만 최소값으로 갱신되고 나머지 초록색 값은 그대로 유지되었다.
그렇게 노드 3과 노드 4의 갱신도 마찬가지로 해주게 되면 최종적인 테이블 나온다
그 결과를 비교해보면,
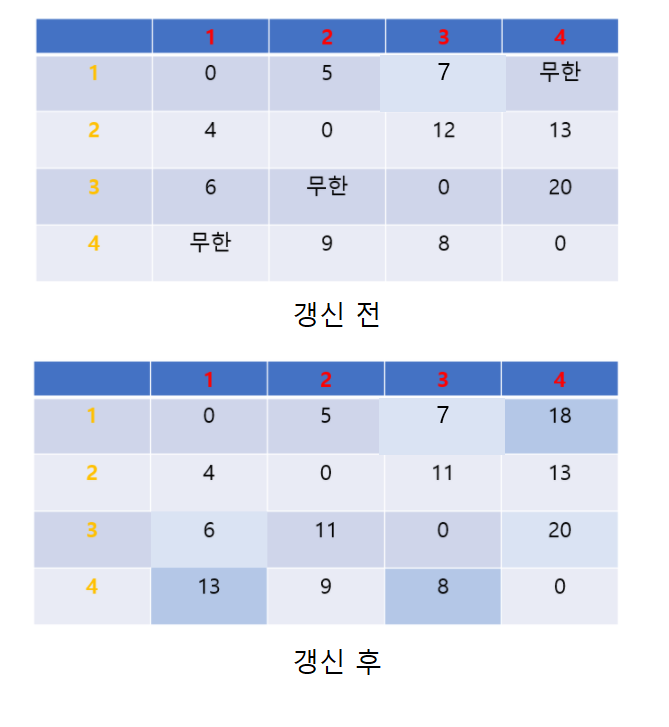
이렇게 모든 정점 노드에서 다른 모든 정점 노드에 대한 데이터를 확인할 수 있게 된다.
코드로 작성해보았다.
#include<iostream>
#define NUMBER 4
#define INFINITE 200000000
using namespace std;
int table[NUMBER][NUMBER] = {
{0,5,7,INFINITE}
,{4,0,12,13}
,{6,INFINITE,0,20}
,{INFINITE,9,8,0}
};
void FloydFunction()
{
for (int k = 0; k < NUMBER; k++) {
for (int i = 0; i < NUMBER; i++)
{
for (int j = 0; j < NUMBER; j++)
{
int temp = table[i][k] + table[k][j];
if (temp < table[i][j])
table[i][j] = temp;
}
}
}
}
void printTable()
{
for (int i = 0; i < NUMBER; i++)
{
for (int j = 0; j < NUMBER; j++)
{
cout << table[i][j]<<" ";
}
cout << endl;
}
}
int main()
{
FloydFunction();
printTable();
return 0;
}결과

갱신 후랑 같은 결과를 볼 수 있다.
