| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 구조적 바인딩
- moreeffectiveC++
- 데이터애셋
- stl
- UE_LOG
- 프로그래머스
- 선택정렬
- 델리게이트
- 람다
- 비동기호출방법
- makeweakobjectptr
- tweakobjectptr
- 스마트포인터
- 크리티컬섹션
- 정렬
- 알고리즘
- unorder_map
- 약참조
- UML관련
- BFS
- 강참조
- map
- C++
- 정렬알고리즘
- enumasByue
- 자료구조
- 애셋로드
- 언리얼가비지컬렉터
- dataasset
- C++최적화
- Today
- Total
기억을 위한 기록들
[알고리즘]크루스칼 알고리즘(Kruskal's Algorithm) 본문
그래프 내의 모든 간선들의 가중치 정보를 사전에 파악하고 이 정보를 토대로 최소 신장 트리를 구축해나가는 것이 특징입니다.
작동 순서
1. 그래프 내의 몯느 간선을 가중치의 오름차순으로 목록을 만듭니다.
2. 1번에서 만든 간선의 목록을 차례대로 순회하면서 간선을 최소 신장 트리에 추가합니다. 단, 이때 추가 된 간선으로 인해 최소 신장 트리 내에 사이클이 형성되면 안됩니다.
해결해야 할 문제
최소 신장 트리에 생기는 사이클을 어떻게 효율적으로 감지 할 것인가?
대안
각 정점들을 각각의 집합 안에 입력하고, 간선으로 연결되어 있는 정점들에 대해서는 합집합을 수행.
이때 간선으로 연결할 두 정점이 같은 집합에 속해 있다면 이 연결은 사이클을 이루게 됨.
예제
사이클 탐지의 문제를 해결 했으니 예제를 통해 크루스칼 알고리즘의 동작 방식을 확인해볼 차례.

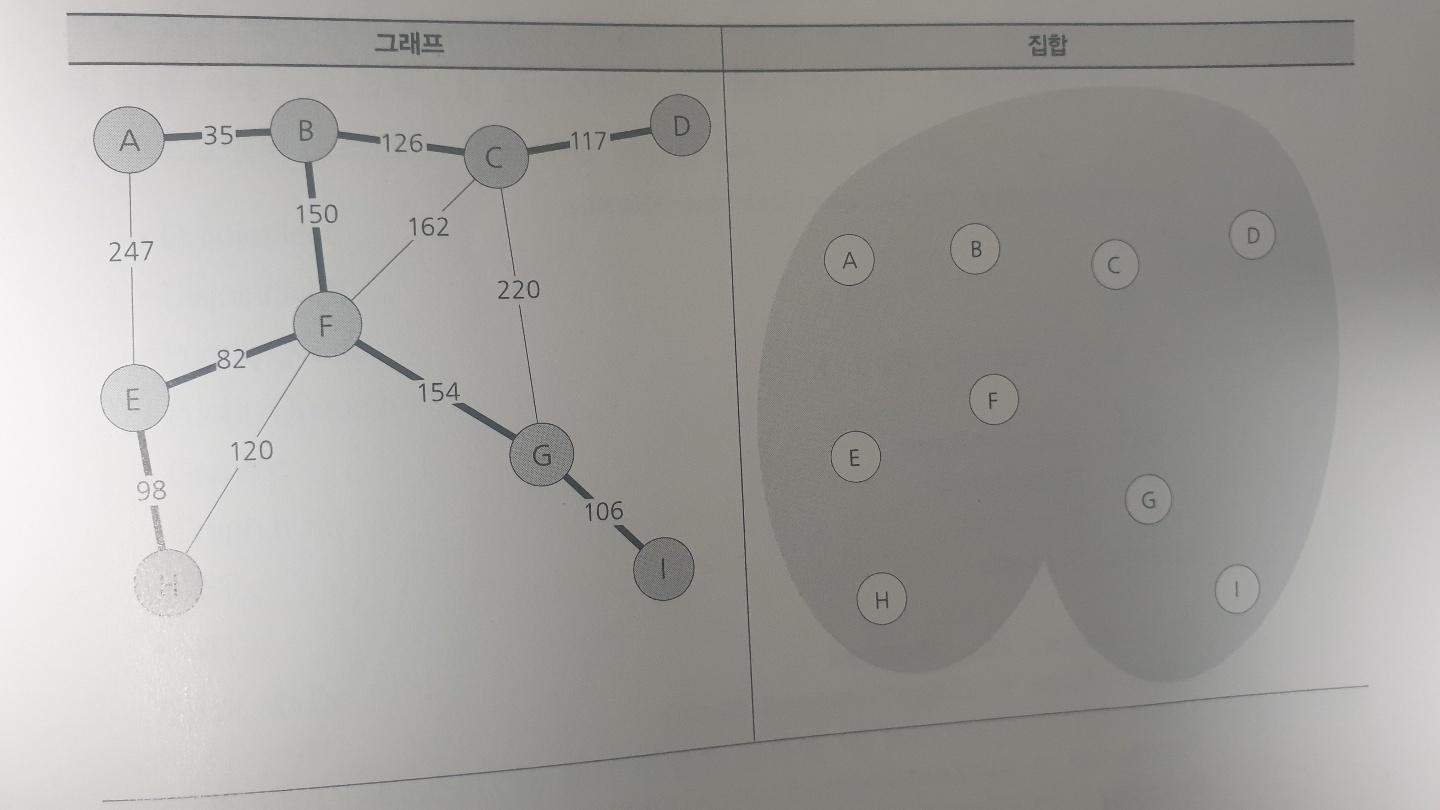
최소 신장 트리를 뽑아낼 그래프이다.
우선 그래프 내의 정점 사이에 있는 모든 간선들이 가중치의 오름차순으로 정렬한다.정렬하면 다음과 같다.
A - B : 35
E - F : 82
E - H : 98
G - I : 106
C - D : 117
F - H : 120
B - C : 126
F - G : 154
C - F : 162
C - G : 220
A - E : 247
이렇게 사전에 가중치 값들을 파악했다.

간선을 가중치 순으로 정하고 각 정점 별로 분리 집합을 만들어주면 준비가 끝난다.
제일 작은 가중치를 갖고 있는 순부터 하면 A-B이다.
이 둘을 최소 신장 트리에 추가하고 간선으로 연결한다. 그리고 분리 집합 A와 B에 대해 합집합을 수행하여 하나의 분리집합으로 만든다.

그 다음으로는 E-F 82, 그 다음으로 G-I 106, 그 다음은 F-H 120 등으로 가중치가 작은 순서대로 묶어준다.

이런식으로 적은 가중치들을 이어주어 가다보면 모든 정점들이 하나의 집합안에 들어가게 되면서 최소 신장 트리가 완성 된다.
프림 알고리즘보다 더 간결해보인다.
참고: 뇌를 자극하는 알고리즘
'자 & 알 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리(MST:Minimum Spanning Tree)란? (0) | 2021.01.27 |
|---|---|
| [알고리즘] 최단 경로찾기 ? 다익스트라 알고리즘 (Dijkstra Algorithm) (0) | 2021.01.27 |
| [알고리즘]프림 알고리즘(Prim'a Algorithm) (0) | 2021.01.27 |
| [알고리즘] 플러드 필(Flood Fill) 알고리즘? (0) | 2021.01.11 |
| [알고리즘] 위상정렬(Topological Sort) (0) | 2021.01.06 |



