| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- map
- 데이터애셋
- 애셋로드
- C++
- 구조적 바인딩
- 정렬알고리즘
- 델리게이트
- 정렬
- 스마트포인터
- C++최적화
- makeweakobjectptr
- 선택정렬
- 프로그래머스
- BFS
- unorder_map
- 강참조
- 알고리즘
- 약참조
- UML관련
- stl
- enumasByue
- tweakobjectptr
- 람다
- 자료구조
- dataasset
- UE_LOG
- 비동기호출방법
- 언리얼가비지컬렉터
- 크리티컬섹션
- moreeffectiveC++
- Today
- Total
기억을 위한 기록들
라디안(radian)이란? 본문
각도의 표현
각도를 표현하는 방법에는 2가지가 있다.
1. 각도법/도수법(dgree)
원주를 360등분 한것으로 하나를 1도로 정한 우리가 흔히 아는 각도이다.
2. 호도법(radian)
호도법을 라디안이라고 하는데, 각도를 나타내는 표현방법이다.
각도에서 호의 길이로 각도를 나타낸다는 발상이다.
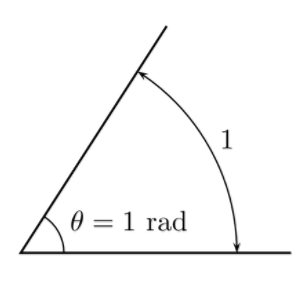
호도법은 호의 길이와 각도를 구하는데 있어서 편리하다.
호의 길이는 구하는 방법을 알아보기전에, 원주의 길이를 구하는 방법을 보면
2 x (원주율) x (반지름)
으로 된다.
원주율은 우리가 흔히 알고 있는 PI(π) 값으로 3.14159265...로 보통 3.14로 인식한다.
다시 짧게 정리하면
2π x 반지름
이렇게 되고
반지름이 1이라면 원주의 길이는 2π 가 된다.
반지름이 1인 원의 원주의 길이는 2π이라는 말은 즉, 360도는 2π이다.
180도의 원주의 길이는 π가된다. 90도는 π/2가 되고 45도는 π/4가된다.
호도법은 간단히 설명하면 "π를 사용하여 180도 각도를 표시하는 것"이다.
호도법은 라디안표기라고도 한다.
확인해보기
위에서 π/4는 45도가 된다고 하였다. 이제 각각의 45도의 원주의 길이를 sin45 ,cos45 ,tan45로 출력되는 값을 확인해보자.
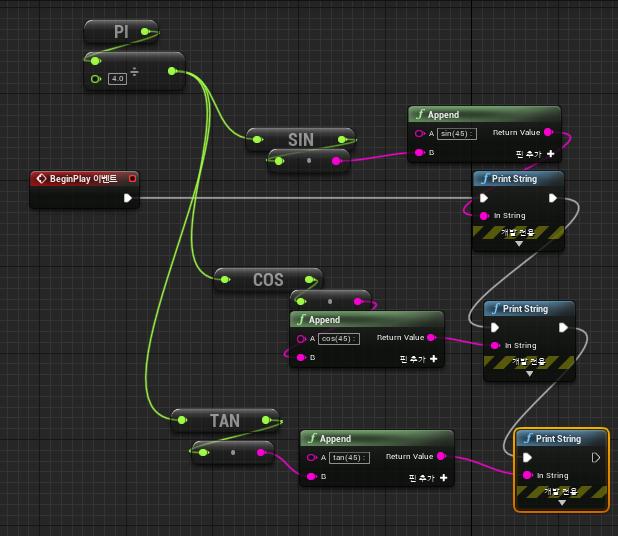

위와 같이 출력된다. 올바르게 계산되었다. 라디안 표기로 각도를 전달하면 제대로 계산되는 것을 알 수있다.
그런데 이렇게 익숙하지 않은 라디안을 사용하게 되면 헷갈릴수 있다.
우리가 흔히 알고 있는 각도값으로 아래와 같은 식으로 라디안 값으로 출력이 가능하다.
π x (각도) / 180.0f
위와 같은 식을 이용하면 원하는 각도를 입력하면 라디안표기로 변경이 가능하다.
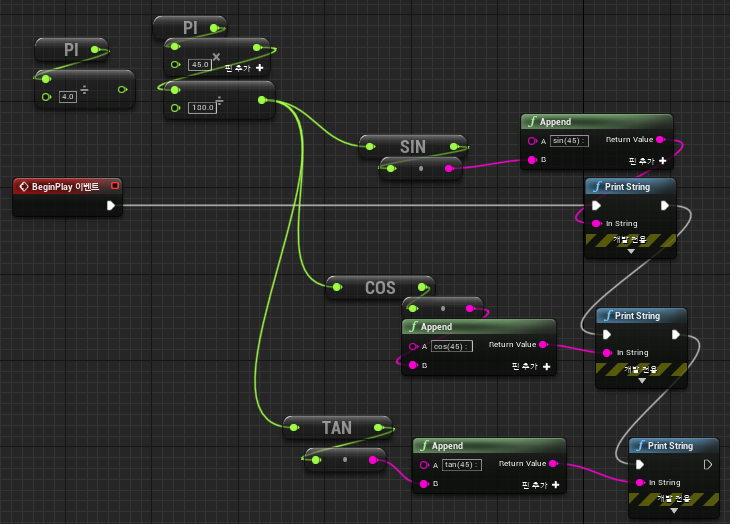
위와 같이해도 이전과 같은 결과값이 나온다.
(사실 언리얼엔진에는 해당 함수가 이미 내장되어 있긴하다.)
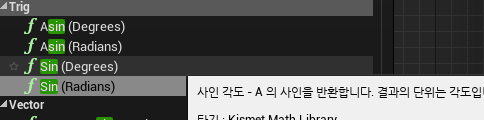
위의 degrees 괄호가 있는 sin 함수를 불러오면(con/tan도 마찬가지) 해당 함수 입력값에 바로 45도를 입력하면 된다. 친절한것같다(?) 아무튼
각도의 정규화
각도는 360도로 한바퀴 돈다. 한바퀴 돌아도 계속 돈다. 예를 들면 370도는 10도와 같고, 720도는 두바퀴 돈것이므로 결국 360와 같은 방향이고 0도이다. 이는 각도 만의 특징으로 프로그램에서 다룰때엔 정규화가 필요하다.
각도의 정규화란
각도 값(라디안)을 0~2π(0~360도)로 만들어버려서 범위에 각도를 제한하는 처리를 의미한다.
예를 들어 정규화가 0~2π로 되어있다고 하면, 3π(540도)를 π(180도)로 바꾸고, -π/2(-90도)는 3π/2(270도)로 바꾼다.
float radian = -0.5f * PI;
radian = rad % (2.0f * PI); //각도를 -2 ~ 2π 범위에 넣는다.
if(radian < 0.0f) //제한하기
{
radian += 2.0f * PI; // 각도를 0 ~ 2π 범위에 넣는다.
}
각도의 정규화를 해주지 않게 되면, 물론 작동은 되겠지만 계속해서 더해주는 회전을 float형 라디안으로 해줬을 때,
계속해서 돌아 float의 값도 커지고, 부동소수점의 정밀도의 문제가 생기게 된다. 각도를 다룰때엔 정규화도 꼭 의식하자.
'그래픽스(Graphics) > Game Math' 카테고리의 다른 글
| 오일러각 (Euler Angles)에 관하여 (0) | 2022.05.10 |
|---|---|
| [3D 게임수학] 5. 아핀공간(Affine Space) (0) | 2021.03.17 |
| [3D 게임수학] 4. 선형 변환(Linear Transformation) (0) | 2021.03.01 |
| 평균/분산/표춘편차 구하기/ O(1)/ C++ (0) | 2021.03.01 |
| [3D 게임수학] 3. 행렬(Matrix) (0) | 2021.02.25 |



