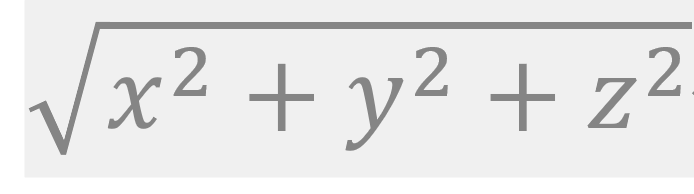| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 스마트포인터
- UE4 커스텀로그
- stl
- 약참조
- 언리얼가비지컬렉터
- 프로그래머스
- UML관련
- 자료구조
- C++최적화
- BFS
- 데이터애셋
- 알고리즘
- 애셋로드
- C++
- enumasByue
- 람다
- map
- 크리티컬섹션
- 정렬
- 람다사용정렬
- 선택정렬
- unorder_map
- 구조적 바인딩
- 델리게이트
- 강참조
- UE_LOG
- UELOG
- dataasset
- 정렬알고리즘
- moreeffectiveC++
- Today
- Total
기억을 위한 기록들
[3D 게임수학] 2. 벡터(Vector) 본문
* 이 글은 개인노트와 같아서 계속해서 수정되고 있습니다. *
아일랜드의 수학자 해밀턴이 1843년, 13년의 연구 끝에 쿼터니언을 발견, 그가 1846년에 발표한 논문에서 쿼터니언의 실수부를 '스칼라', 허수부를 '벡터'라고 말하면서 비로소 벡터라는 용어가 생겼다.
유클리드 공간(Euclidean Space)
유클리드라는 기원전 300년경에 살았던 그리스의 수학자이다.
20세기 초까지 그의 책 '원론'은 수학, 특히 기하학을 가르치는 교과서로 쓰였다.
'원론'에서 나온 공리들 중 일부이다.
- 임의의 점과 다른 한 점을 연결하는 직선은 단 하나뿐이다.
- 임의의 선분은 양 끝으로 얼마든지 연장할 수 있다.
- 임의의 점을 중심으로 하고 임의의 길이를 반지름으로 하는 원을 그릴 수 있다.
하지만, 우리는 유클리드 공간을 '원론'에 있는 그대로가 아닌 17세기 프랑스 구학자인 데카르트가 만든 "카르테지안 좌표계(직교 좌표계)"를 사용해서 배운다.
유클리드의 가하학은 어떤 구체적인 양을 다루지 않고 있기에 다소 추상적이었다.
하지만, 카르테지안 좌표계를 사용해서 구체적인 양을 도식화하여 도형들을 수식으로 표현할 수 있고, 이는 카르테지안 좌표계가 대수와 유클리드기하학을 연결하는 엄청난 수학적 발명임을 말해준다.
실수(real number)로 이루어진 2차원 평면 R^2 과 3차원 공간 R^3 라는것을 의미
3차원 공간에서의 벡터
3차원 공간은 엄밀히 말해서 아핀공간(Affine Space)이다.
아핀공간은 벡터만 있는것이 아니라 점(Point)이 같이 있는 공간이다. 하지만 흔히 3차원 공간은 벡터 공간이라고 토용되고 있다.
- 3차원 공간에서 벡터는 크기(길이)와 방향을 가진 것으로 일종의 화살표가 있는 직선이라고 생각할 수 있다.
- 벡터는 위치 개념이 없다.(길이와 방향이 같으면 어디에 위치하든 같은 벡터)
- 벡터의 크기가 1이면, 이 벡터를 단위 벡터(unit vector)라고 한다.
- 길이가 0인 벡터는 영 벡터(zero vector/null vector)라고 한다.
- 벡터 공간을 이루는 벡터들은 연산은 두가지 벡터 덧셈과 스칼라 곱셉이 존재한다. (벡터 공간을 정의하기 위한 체는 실수체)

3차원 공간의 벡터를 수식안에서 어떻게 표현할지?
선형조합(linear combination)과 기저(basis)에 대한 이해가 필요.
ex)
어떤 벡터들의 집합 S = {v1,v2,...,vn}이 있으면, 선형조합은 다음과 같이 나타낼 수 있다.
v = s1 * v1 + s2 * v2 + ... + sn * vn
여기서 s1,s2,s3...sn은 임의의 스칼라 값들이다.
여기서 선형조합(linear combination)이란?
집합 각각의 원소에 임의의 스칼라값들을 곱한 후 모두 더한 것들을 말함.
임의로 스칼라 값을고르니 무수한 선형조합이 있을수 있다.
S에서 가능한 모든 선형조합들로 생겨난 결과들을 다시 하나의 집합으로 묶었다고 해보자. 이때, 만약 이 집합이 벡터 공간 T를 이룬다면 우리는 S가 벡터 공간 T를 생성(span)한다고 한다.
S가 어떤 특정 조건을 만족하면 S를 T의 기저(basis)라고 하며, S의 각 원소들은 기저 벡터(basis vector)라고 불린다.
어떤 특정조건이란?
바로 S의 한 원소가 나머지 원소들의 선형 조합으로는 만들어 질 수 없어야 한다는 것.
(이는 S의 원소들이 서로에 대해 선형독립(linear independent)이어야 한다는 것과 같은 말이다.
(즉, v1는 어떤 스칼라 값들을 사용한다 해도 나머지 벡터 v2,v3,v4...vn들의 선형조합으로는 결코 만들어 질수 없다는 의미)
표준기저(standard basis)란?
모든 원소들의 길이가 1이고, 원소들이 각각의 직교 좌표계 축의 양의 방향을 가리키는 경우
벡터의 뺄셈
벡터에 -1를 곱한 후 덧셈을 하는것과 같다. -1를 곱한다는 것은 기하학적으로 벡터의 방향을 반대로 바꾸는 것으로 생각할 수 있다.
벡터의 크기(길이) 구하기
원점에서 부터 (x,y,z)까지의 직선의 길이가 바로 벡터의 크기가 된다. 피타고라스의 정리를 사용하면 된다.
블로그에서 루트쓰는 방법을 모르겠다..
단위 벡터(정규화/nomalize)만들기
각 성분들 위에서 구한 벡터의 크기(길이)로 나누면 된다. 이를 벡터의 정규화(nomalize)라고 한다.(벡터의 노말값이라고 말했다). 정규화는 벡터의 방향을 똑같이 유지하면서 길이만 1로 만든 것이다.
단위벡터 = 벡터/벡터의 크기
벡터내적 (Dot Product)
- 벡터의 내적은 두 벡터를 가지고 한 스칼라 값을 구하는 연산
- 그라스만이라는 수학자가 논문에 '선형 곱(Linear product)'이라는 걸 소개 했는데 이게 바로 벡터의 내적이다.
- 결과가 스칼라로 나오기때문에 스칼라 곱이라고 부르기도 한다.
벡터 A * 벡터 B = 벡터A의 길이 * 벡터B의 길이 * cosθ
벡터 A와 B의 길이가 1이라면,
벡터 A * 벡터 B = cosθ
더 간단하게 구하는 방법은 두개의 벡터의 각각의 x,y,z요소를 서로 곱해주고 모든 값을 더하면 된다.
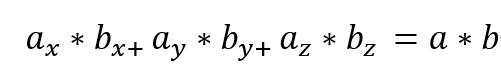
한 벡터가 자기 자신과 내적하면 자기 자신 벡터의 길이의 제곱이 된다.
- 내적이 0이면 두 벡터의 사이 값은 90도이다.
- 내적이 0보다 크면 사이각이 90보다 작고,
- 내적이 0보다 작으면 사이각이 90보다 크다.
내적의 활용
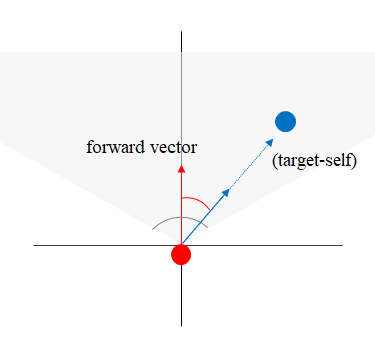
1. 게임에서의 활용(앞뒤 판별)
주인공캐릭터의 방향 벡터와 주인공의 위치에서
적을 향하는 벡터를 내적하여 결과가 양이면 적이 주인공 앞에 있고, 반대로 음수이면 주인공 뒤에 있다.
2. 게임에서의 활용(시야각 판별)
플레이어의 시야각 a가 있다고 하면 적을 향하고 있는 캐릭터의 정면벡터에서 타겟까지의 각이
전체 시야각 2/a 보다 작으면 시야이내에 있는것을 알 수 있다.
3. 투영 벡터
어떤 벡터를 다른 벡터에 투영한 결과 벡터를 계산할때이다.
아래 벡터a를 벡터 b에 투영한 결과는 ||?|| 라고하자. (||?|| 는 ? 벡터의 크기)
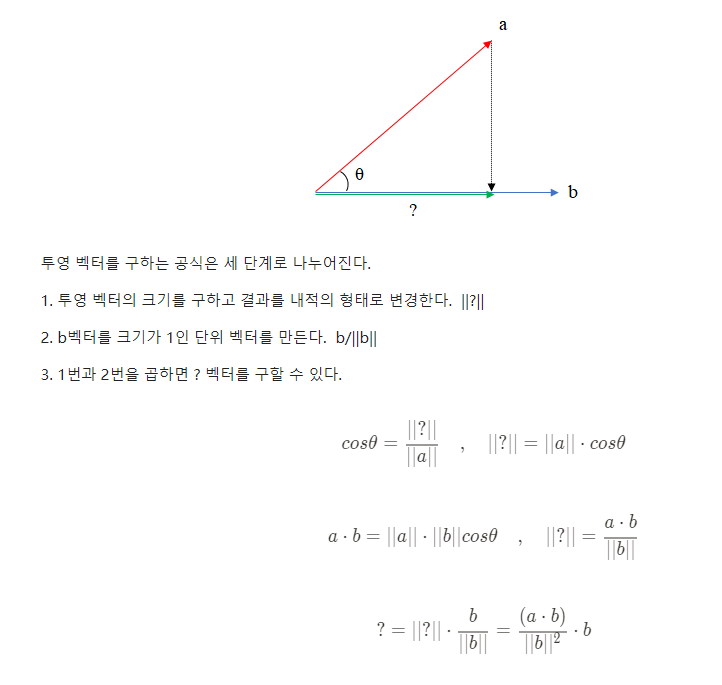
컴퓨터에서 사인 이나 코사인 값을 직접 계산하는 것은 큰 연산 비용을 요구한다.
하지만 내적을 사용하면 컴퓨터가 가장 빠르고 잘 할 수 있는 곱셈과 덧셈의 연산 문제로 귀결된다. 따라서 코사인 함수가 나오는 공식은 모두 내적으로 변경하는 것이 바람직하다.
[출처] 13. 벡터의 내적(Dot Product)|작성자 이득우 / https://blog.naver.com/destiny9720/221407625806
13. 벡터의 내적(Dot Product)
안녕하세요. 2018년 (무려 4년전.. )에 연재한 상상하는 게임 수학에 설명한 내용을 모아 책으로 발간했습...
blog.naver.com
벡터외적 (Cross Product)
내적과 마찬가지로 수학자 그리스만이 발표한 논문에서 소개 된 바로, 벡터의 외적은 두 벡터를 가지고 다른 벡터를 만드는 연산이다. 이렇게 만들어진 벡터는 처음 주어진 두 벡터 모두에게 수직이 된다.
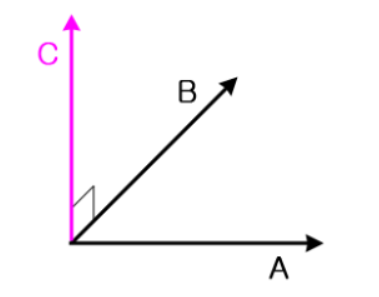
벡터 C의 크기 = 벡터A * 벡터 B * sinθ
외적의 특성
- x + (y + z) = (x * y) + (x * z)
- a * (x * y) = (a * x) * y = x * (a * y)
- x * 0 = 0 * x = 0
- x * x =0
외적의 활용
1. 법선벡터(Nomal Vector) 구할 때
3차원에서 평면을 표현할 때, 평면상의 한 점과 평면과 수직인 벡터를 법선 벡터라고 한다.
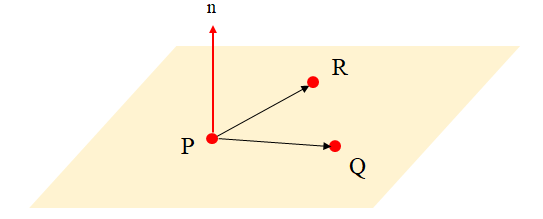
n이 법선 벡터가 된다.
2. 평행 여부 판단
두 벡터가 서로 평핸하다면 두 벡터의 외적으로 나온 벡터의 크기는 0이 된다. (두 벡터의 사이각이 0이나 180도 이어야하며, 사이각의 sin 값은 0이 된다.)
(벡터의 크기의 제곱은 자기 사긴과의 내적과 같다고 했다. 다음 과 같이 판단 가능하다)
(a*b)*(a*b)=0이면 벡터a와 b는 평행이다.
3. 카메라의 행렬을 구할 때,


4. 게임에서의 활용(왼쪽 오른쪽 판별)
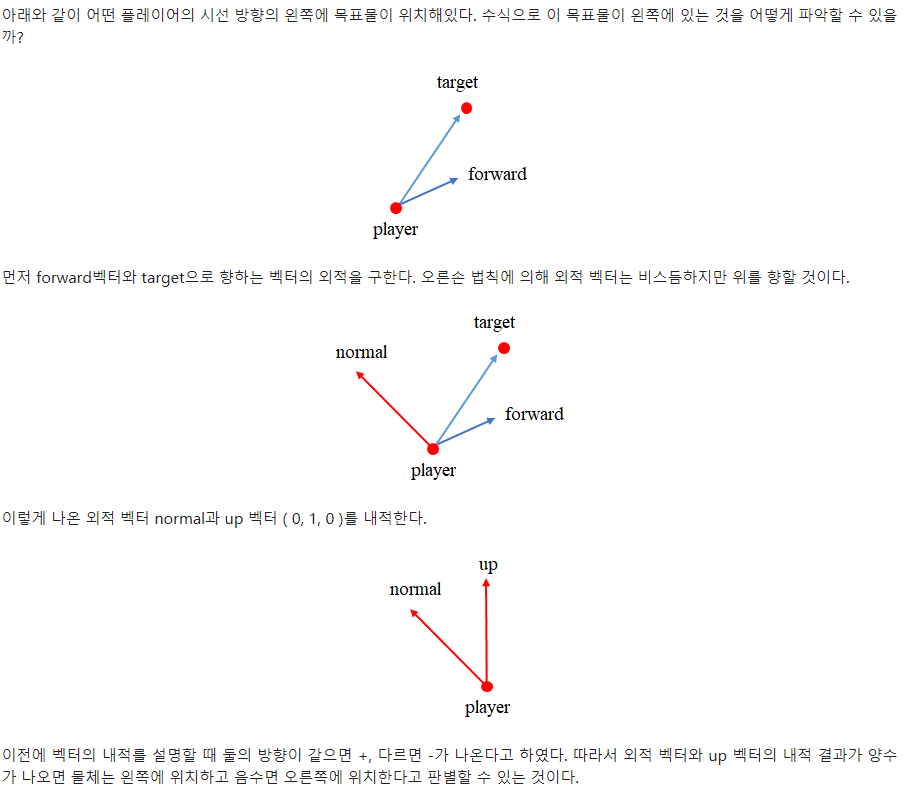
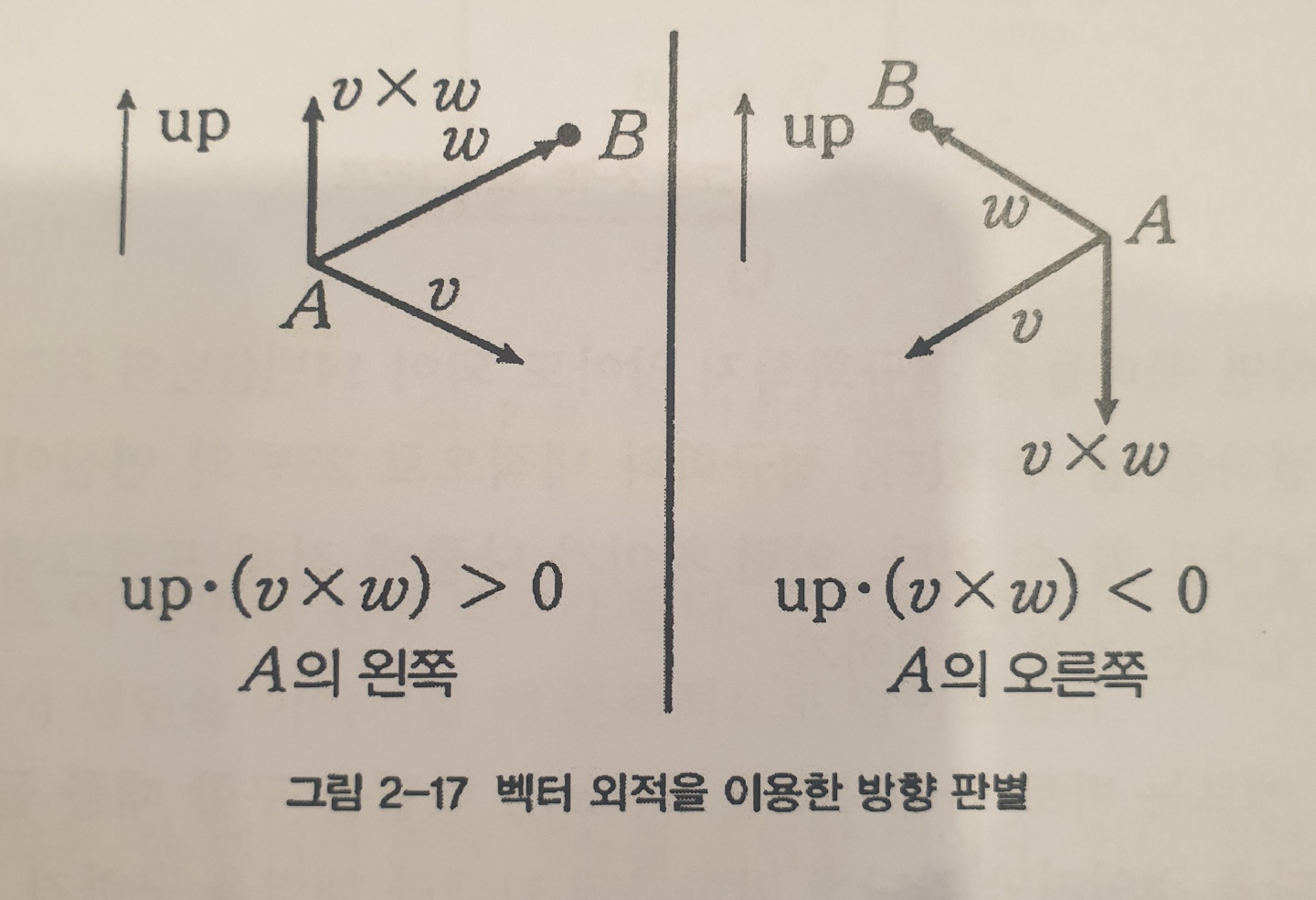
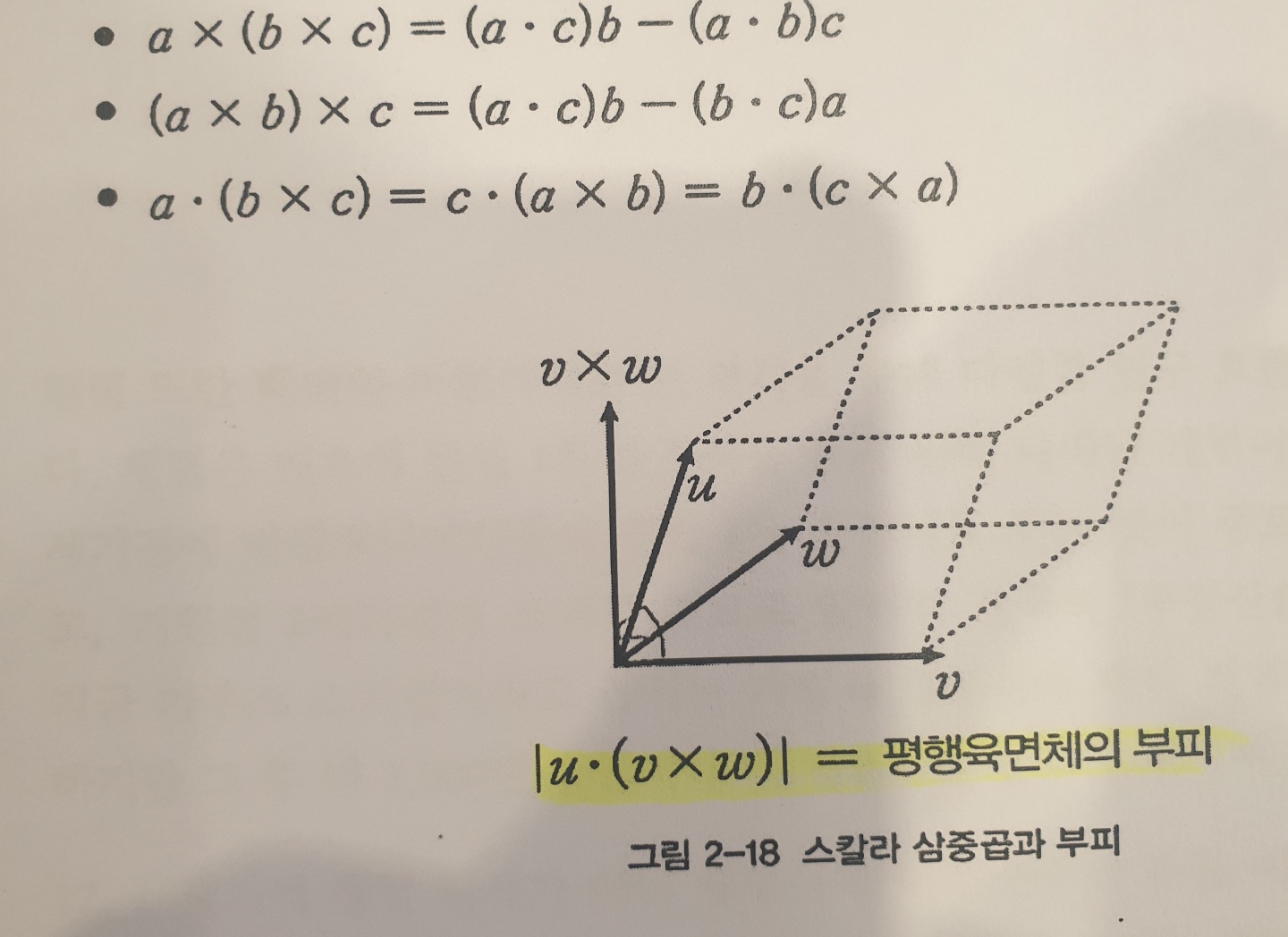
사실 위에서 사용한 u*(vXw)연산은 스칼라 삼중곱이라는 정식 명칭이 있다.
스칼라 삼중곱은 다음과 같은 성질을 가지고 있다.
a*(bXc) = b*(cXa) = c*(aXb) = det(a,b,c)
det(a,b,c)는 행렬의 행렬식을 의미한다.
외적은 두 벡터가 이루는 평행사변형의 넓이와 관련이 있다. 스칼라 삼중곱은 세 벡터가 이루는 평행육면체의 부피를 의미한다.
'그래픽스(Graphics) > Game Math' 카테고리의 다른 글
| 평균/분산/표춘편차 구하기/ O(1)/ C++ (0) | 2021.03.01 |
|---|---|
| [3D 게임수학] 3. 행렬(Matrix) (0) | 2021.02.25 |
| [3D 게임수학] 1. 선형대수(Linear Algerbra) (0) | 2021.02.08 |
| UE4 쿼터니온 활용 참고 (0) | 2020.05.18 |
| Quaternion (쿼터니온/사원수) (0) | 2020.05.13 |