| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 스마트포인터
- tweakobjectptr
- dataasset
- C++최적화
- unorder_map
- 람다
- 약참조
- 구조적 바인딩
- 크리티컬섹션
- moreeffectiveC++
- stl
- 프로그래머스
- 언리얼가비지컬렉터
- 애셋로드
- 데이터애셋
- 정렬
- 선택정렬
- 비동기호출방법
- 자료구조
- UE_LOG
- UML관련
- BFS
- 델리게이트
- map
- C++
- enumasByue
- 강참조
- makeweakobjectptr
- 알고리즘
- 정렬알고리즘
- Today
- Total
기억을 위한 기록들
[자료구조] 힙(Heap)구현(for 우선순위 큐)/ C++ / (+함수포인터 변수) 본문
hyo-ue4study.tistory.com/127?category=907498
힙(Heap) 특징
힙은 완전 이진트리 자료구조의 일종. 힙에서는 항상 루트노드를 제거. 최소 힙 : 루트 노드가 가장 작은 값/ 값이 작은 데이터가 우선적으로 제거 최대 힙 : 루트 노드가 가장 큰값/ 값이 가장 큰
hyo-ue4study.tistory.com
hyo-ue4study.tistory.com/189?category=862971
[C++]STL 우선순위 큐(priority_queue)
0. 기본 우선순위는 less (내림차순 높은값이 루트값) #include #include #include using namespace std; int main() { //priority_queue<자료형,컨테이너 타입,우선순위> //아무것도 입력하지 않으면 기본 정렬은..
hyo-ue4study.tistory.com
- 힙의 구현은 우선순위 큐의 완성으로 이어진다.힙과 우선순위 큐를 동일하게 인식하는 경향이 매우 강하다.
하지만, 이는 정확 하지 않으니, 우선순위 큐와 힙을 어느정도 구분할 수 있으면 좋겠다.
힙은 우선순위 큐에 딱 어울리는, 완전 이진트리의 일종이라는 사실을 기억하자.
- 우선순위 큐??
우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조이다.
추출되는 데이터로는 스택은 가장 나중에 삽입된 데이터 삭제, 큐는 가장 먼저 삽입된 데이터, 그리고 우선순위 큐는 가장 우선순위가 높은 데이터를 삭제한다.
- 힙 중에서 최대 힙과 최소힙으로 우선순위 큐로 사용하기 좋은 자료구조이다.
- 힙은 연결 리스트를 기반으로 구현가능, 그러나 새로운 노드를 힙의 '마지막 위치'에 추가하는 것이 쉽지않다.
사소한 이유 같고, 연결리스트로 쉽게 해결 될 것 같으나, 결코 간단하지 않다. 그래서 배열로 트리를 구현해본다.
- 배열에서의 k번 인덱스에 위치한 노드의 양쪽 자식들이 위치한 인덱스
왼쪽 자식노드 : 2k+1
오른쪽 자식노드 : 2k +2
-k번 인덱의에 위치한 노드의 부모 노드가 위치한 인덱스 : (k-1) / 2의 몫
상단 부분과
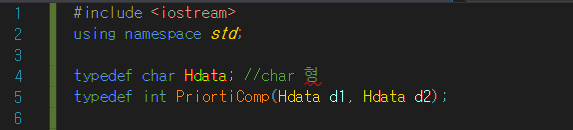
Class 선언부

HeapInit/Insert/Delete 부분

IsEmpty/GetHipriChildIDX 부분
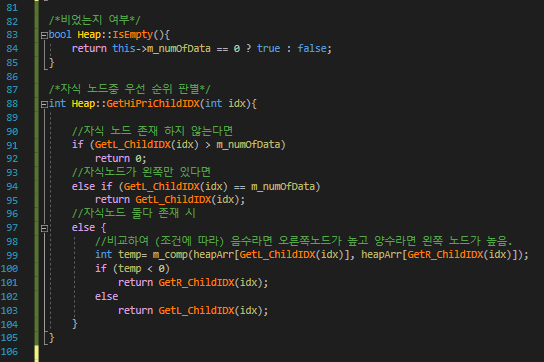
* 우선순위 판별시 순서가
자식노드 존재 x -> 왼쪽 노드만 존재 ->둘다 존재 인데
왼쪽 노드만 있는지 여부를 검사하는 이유는 힙은 완전 이진 트리이므로, 하나뿐인 자식 노드는 왼쪽 자식 노드이며, 그리고 해당 힙의 마지막 노드이기 때문이다.
등록되는 함수와 main 함수 부분

넣은 알파벳 순서는 뒤죽 박죽(?)이지만,
결과 값은

정렬되어 출력된다.
#include <iostream>
using namespace std;
typedef char Hdata; //char 형
typedef int PriortiComp(Hdata d1, Hdata d2);
class Heap {
public:
void HeapInit(PriortiComp pc); //생성
void Insert(Hdata data); //삽입
Hdata Delete(); //삭제
bool IsEmpty() const; //비어있는지
public:
int GetParentIDX(int idx) { return (idx - 1) / 2; } //부모 인덱스 번호 반환
int GetL_ChildIDX(int idx) { return (idx * 2) + 1; } //자식 - 왼쪽 인덱스 반환
int GetR_ChildIDX(int idx) { return (idx * 2) + 2; } //자식 -오른쪽 인덱스 반환
int GetHiPriChildIDX(int idx); //자식 중 우선순위 높은 인덱스 반환
private:
PriortiComp* m_comp;
int m_numOfData;
Hdata heapArr[100];
};
/*생성*/
void Heap::HeapInit(PriortiComp _pc)
{
this->m_numOfData = 0;
this->m_comp = _pc; //우선순위 비교에 사용되는 함수 등록
}
/*삽입*/
void Heap::Insert(Hdata _data)
{
int idx = m_numOfData + 1; //기존 데이터 값의 다음 자리로 초기화
/*저장 될 위치가 루트노드가 아니라면 반복문 실행*/
while (idx != 1) {
int temp = m_comp(_data, heapArr[GetParentIDX(idx)]); //부모노드와 데이터 값 비교 결과
if (temp > 0)//우선순위 비교 성공 시 자리 바뀜
{
heapArr[idx] = heapArr[GetParentIDX(idx)]; //부모노드를 한단계 내림
idx = GetParentIDX(idx); //새노드를 한 레벨 올림(실제로 아니고 인덱스 값만)
}
else
{
break; //새 노드의 우선순위가 높지 않다면 탈출
}
}
heapArr[idx] = _data; //해당 인덱스 값에 저장
m_numOfData++; //값 증가
}
Hdata Heap::Delete()
{
Hdata retData = heapArr[1]; //삭제할 노드 임시저장
Hdata lastElem = heapArr[m_numOfData]; //해당 힙의 마지막 노드
int parantIdx = 1;//루트의 인덱스 값
int childIdx = 0;
//루트 노드의 우선순위가 높은 자식 노드를 시작으로 반복 시작
while (childIdx = GetHiPriChildIDX(parantIdx))
{
//마지막노드 우선순위 먼저 비교
int temp = m_comp(lastElem, heapArr[childIdx]);
if (temp >= 0) //마지막 노드의 우선순위가 높으면 탈출
break;
//우선순위가 높으니 한단계 상승
heapArr[parantIdx] = heapArr[childIdx];
parantIdx = childIdx;
}
heapArr[parantIdx] = lastElem;
m_numOfData--;
return retData;
}
/*비었는지 여부*/
bool Heap::IsEmpty() const
{
return this->m_numOfData == 0 ? true : false;
}
/*자식 노드중 우선 순위 판별*/
int Heap::GetHiPriChildIDX(int idx)
{
//자식 노드 존재 하지 않는다면
if (GetL_ChildIDX(idx) > m_numOfData)
return 0;
//자식노드가 왼쪽만 있다면
else if (GetL_ChildIDX(idx) == m_numOfData)
return GetL_ChildIDX(idx);
//자식노드 둘다 존재 시
else
{
//비교하여 (조건에 따라) 음수라면 오른쪽노드가 높고 양수라면 왼쪽 노드가 높음.
int temp = m_comp(heapArr[GetL_ChildIDX(idx)], heapArr[GetR_ChildIDX(idx)]);
if (temp < 0)
return GetR_ChildIDX(idx);
else
return GetL_ChildIDX(idx);
}
}
int DataPriortiComp(char ch1, char ch2)
{
return ch2 - ch1; //아스키코드 계산에 따라..
}
int main() {
Heap heap;
heap.HeapInit(DataPriortiComp);
heap.Insert('A');
heap.Insert('C');
heap.Insert('A');
heap.Insert('B');
heap.Insert('C');
while (!heap.IsEmpty())
cout << heap.Delete() << endl;
return 0;
}
-참고 윤성우의 열혈 자료 구조 -
'자 & 알 > 자료구조' 카테고리의 다른 글
| [자료구조] 재귀를 이용한 트리운행/스택을 이용한 트리운행 (0) | 2021.04.01 |
|---|---|
| [자료구조] 그래프(Graph)에 관하여 (0) | 2021.01.06 |
| [자료구조] 힙(Heap) 특징 (0) | 2021.01.03 |
| [자료구조]연결리스트-양방향 DLL(DoublyLinkedList) / 템플릿 /C++ (0) | 2020.12.25 |
| [자료구조]연결리스트 SLL(SinglyLinkedList) / 템플릿 /C++ (0) | 2020.12.20 |




