| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 정렬알고리즘
- 비동기호출방법
- 알고리즘
- 정렬
- 프로그래머스
- 스마트포인터
- C++최적화
- 데이터애셋
- enumasByue
- map
- C++
- 자료구조
- 애셋로드
- BFS
- 구조적 바인딩
- 강참조
- 약참조
- 언리얼가비지컬렉터
- UELOG
- moreeffectiveC++
- UML관련
- dataasset
- stl
- UE4 커스텀로그
- 선택정렬
- 델리게이트
- UE_LOG
- unorder_map
- 람다
- 크리티컬섹션
- Today
- Total
기억을 위한 기록들
[자료구조] 그래프(Graph)에 관하여 본문
정점 : 지점을 나타낸것
간선 : 2개 이상의 정점을 연결한 것
인접(Adjacent) : 나와 이웃하고 있는 정점
경로(Path) : 한 정점에서 다른 정점까지의 길
사이클(Cycle) : 단순 경로의 시작과 종료 정점이 동일한 경로
연결성 : 모든 정점이 서로 연결되어 있는것
방향성 그래프(Directed Graph) : 간선이 방향성을 가짐.
무방향성 그래프(Undirected Graph) : 간선에 방향성이 없음.
그래프는 정점의 집합? 간선의 집합?
정점의 집합 표현 방법 : 배열, 링크드 리스트 등
간선의 집합 표현 방법 : 간선은 그냥 선이 아니라 '인접관계'를 나타냄. 그래서 인접행렬(Adjacent Matrix) 또는 인접리스트(Adjacent List)로 표현
간선의 집한 표현방법 2가지
1. 인접행렬(Adjacent Matrix)
정점의 수가 N이라면 N x N 크기의 행렬을 만듦. 행렬의 각 원소를 한 정점과 또 다른 정점이 인접해 있는 경우(즉, 정점 사이에 간선이 존재)에는 1로 표시, 인접해 있지 않으면 0으로 표시.

무방향성 그래프인 경우에는 아래처럼 대각선에 대해 대칭을 이루는 것이 특징. (방향성 그래프는 그렇지 않음)

2. 인접리스트(Adjacent List)
인접행렬과 같이 그래프내의 인접관계를 표현하는 리스트. 각 정점이 자신과 인접해 있는 모든 정점의 목록을 리스트로 관리.
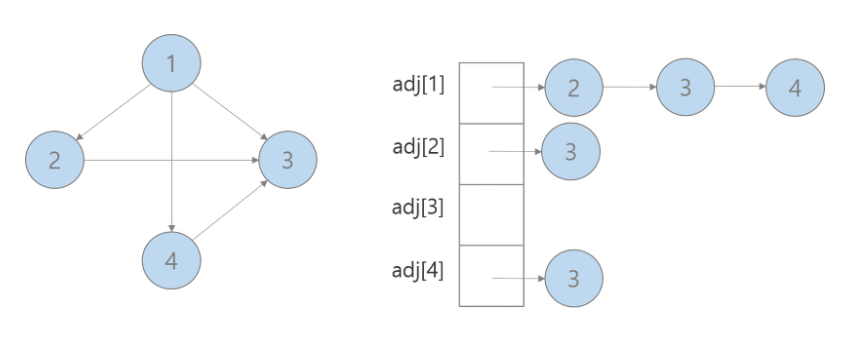
인접행렬 VS 인접리스트
그래프내의 정점의 수가 많지 않거나, 정점끼리의 인접 여부를 빠르게 알아내야한다면 인접행렬 사용,
정점과 간선의 입력이 빈번하게 이루어지고, 메모리 효율성을 우선시 해야한다면 인접리스트 사용.
그래프에서의 탐색
hyo-ue4study.tistory.com/74?category=951082
깊이 우선 탐색(Depth First Search) & 너비우선탐색(Breadth First Search)/ C++
깊이 우선 탐색(DFS) - 스택활용 (or 재귀) 최상단노드부터 말단 노드까지 빠르게 내려가면서 탐색하는 방법으로 보통 경우의 수를 확인 할 때 (사용 예: 바둑, 장기 등) 장점 :하나의 말단 노드까지
hyo-ue4study.tistory.com
'자 & 알 > 자료구조' 카테고리의 다른 글
| [자료구조] std::map & std::unordered_map 개념 (0) | 2021.08.16 |
|---|---|
| [자료구조] 재귀를 이용한 트리운행/스택을 이용한 트리운행 (0) | 2021.04.01 |
| [자료구조] 힙(Heap)구현(for 우선순위 큐)/ C++ / (+함수포인터 변수) (0) | 2021.01.03 |
| [자료구조] 힙(Heap) 특징 (0) | 2021.01.03 |
| [자료구조]연결리스트-양방향 DLL(DoublyLinkedList) / 템플릿 /C++ (0) | 2020.12.25 |




